Recently, I've been learning geo algorithms for developing a geometry library. However, I found that the materials of 2d geometry algorithms on the internet ara complicated and messy since I only want to find several basic and commonly used algorithms. Here, I will try my best to make 2d geometry algorithms below easy to be understood and used.

By the way, you may not be necessary to read this article paragraph by paragraph, you can just read any topic which you prefer. Here we go!

Transformation

Translation

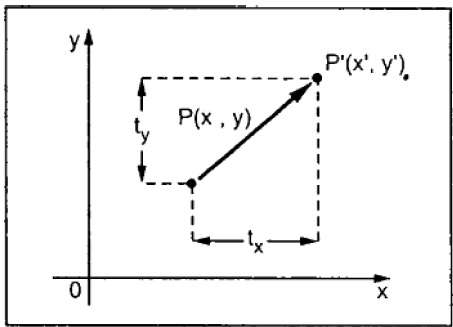
Suppose we move point's position from (x, y) to (x', y'):

x ' = x + t _ x

y ' = y + t _ y

Scale

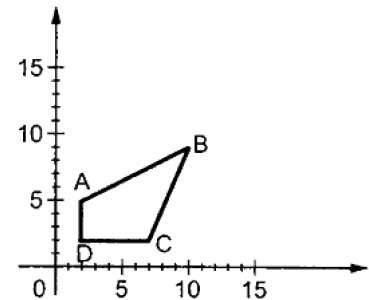
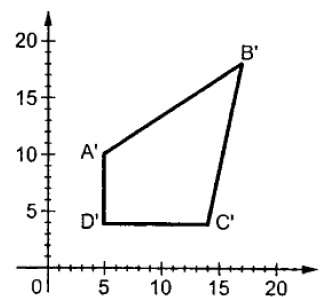
Suppose we scale the x of point by sx times and the y of point by sy times, then:

x ' = s _ x * x

y ' = s _ y * y

Scale point based on a center point (xc, yc)

x ' = s _ x * x - ( s _ x * x _ c - x _ c )

y ' = s _ y * y - ( s _ y * y _ c - y _ c )

Rotation

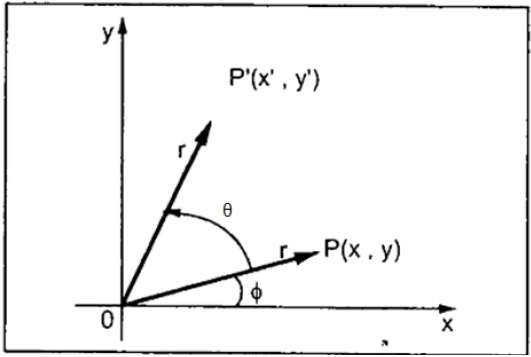
Suppose we rotate OP to OP'.
Because:

x = r \cdot cos \varphi

y = r \cdot sin \varphi

Then:

x' = r \cdot cos ( \varphi + \theta ) = r \cdot ( cos \varphi \cdot cos \theta - sin \varphi \cdot sin \theta ) = x \cdot cos \theta - y \cdot sin \theta

y' = r \cdot sin ( \varphi + \theta ) = r \cdot ( sin \varphi \cdot cos \theta + cos \varphi \cdot sin \theta ) = x \cdot sin \theta + y \cdot cos \theta

Rotate point based on a center point (xc, yc)

x' =  x \cdot cos \theta - y \cdot sin \theta + xc

y' = x \cdot sin \theta + y \cdot cos \theta + yc

Point in polygon

In fact, there're two well-known "point in polygon" algorithms: winding number and crossing number, however, I will only talk about winding number, here are reasons:

As we can see above, crossing number is not suitable for all polygons.

Winding number

Draw an infinite ray from P crossing polygon, then count each vertex, here's the key: suppose we start at any point on polygon path and end at the same point to draw polygon counterclockwise, if the vector intersected the special vertex(intersected by infinite ray and polygon) is upward, wn adds 1, otherwise if the track intersected vertex is downward, wn subtracts 1. If the wn of P is not 0, then P is inside of polygon, otherwise P is outside.
Main javascript(typescript) codes(If you want to see whole detail code, visit here):

/**
 * Check if point P is inside of polygon with winding number algorithm
 * Algorithm: http://geomalgorithms.com/a03-_inclusion.html
 * @param {Point2D} P point P
 * @param {Point2D[]} polygonVertices vertices of polygon path in clockwise or counterclockwise order
 */
function pointInPolygonWindingNumber(
  P: Point2D,
  polygonVertices: Point2D[]
) {
  /**
   * Winding nunebr
   */
  let wn = 0

  const points: Point2D[] = polygonVertices

  for ( let i: number = 0; i < points.length - 1; i++ ) {
    const V0: Point2D = points[ i ]
    const V1: Point2D = points[ i + 1 ]

    const { x: x0, y: y0 }: Point2D = V0
    const { x: x1, y: y1 }: Point2D = V1
    const { x: xp, y: yp }: Point2D = P

    /**
     * Upward
     */
    if ( y0 <= yp && y1 > yp && isLeft( V0, V1, P ) ) {
      wn = wn + 1
    }
    /**
     * Downward
     */
    if ( y0 > yp && y1 <= yp && isRight( V0, V1, P ) ) {
      wn = wn - 1
    }
  }

  const pointOnPolygonPath: boolean = isPointOnPolygonPath( P, points )
  const res: boolean = pointOnPolygonPath || wn !== 0

  return res
}

Matrix

I'm curious about matrices too, not only when learning geometry algorithms. Matrix, which like an magician, transforms geometry with its particular formula.

Translation

\begin{bmatrix}
   x' \\
   y'
\end{bmatrix}
=
\begin{bmatrix}
   x \\
   y
\end{bmatrix}
+
\begin{bmatrix}
   tx \\
   ty
\end{bmatrix}

Scale

\begin{bmatrix}
   x' \\
   y'
\end{bmatrix}
=
\begin{bmatrix}
   S _ x & 0 \\
   0 & S _ y
\end{bmatrix}
\begin{bmatrix}
   x \\
   y
\end{bmatrix}

Rotation

\begin{bmatrix}
   x' \\
   y'
\end{bmatrix}
=
\begin{bmatrix}
  cos \theta & -sin \theta \\
  sin \theta & cos \theta
\end{bmatrix}
\begin{bmatrix}
   x \\
   y
\end{bmatrix}

Formulas

There are plenty of geometry algorithms, however, I only list several alogorithms which are frequently used above. Maybe, I say maybe, I will add new algorithms in this blog if I find new commonly used algorithm in the future. Nevertheless, I'll still list some practical formulas which can be used for geometry calculation.

The Cosine Law

Suppose there are vector v and w

| v \pm w | ^ 2 = | v | ^ 2 \pm 2 | v | | w | cos( \theta ) + | w | ^ 2

The Dot Product

One vector multiply the other vector:

v \cdot w = | v | | w | cos ( \theta )

The 2D Perp Product

v \perp w = | v | | w | sin ( \theta )

Computing area

• Parallelogram

A ( \Box ) = | v \perp w | 

    = |v| |w| sin( \theta )

• Triangles

A ( \vartriangle ) = | v \perp w | / 2t

    = |v| |w| sin( \theta ) / 2

Lines formula

• Type-Parametric

P(t) = P _ 0 + t v _ L 

• Line equations

P ( t ) = P _ 0 + t v _ L 

    = P _ 0 + t ( P _ 1 - P _ 0 )

    = ( 1 - t ) P _ 0 + t P _ 1

    = ( x _ 0 + t cos \theta , y _ 0 + t sin \theta ) 

It's easy to learn and use a geometry library, however, it's limited when we want to build a large or complex even just a little complex project. Grasping geometry algorithms will make it possible for us to create flexible and large geometry projects.

Reference

[0] Transformation: https://www.tutorialspoint.com/computer_graphics/2d_transformation.htm
[1] Point in polygon1: https://en.wikipedia.org/wiki/Point_in_polygon
[2] Point in polygon2: http://geomalgorithms.com/a03-_inclusion.html
[3] Nonezero-rule: https://en.wikipedia.org/wiki/Nonzero-rule
[4] Even-odd rule: https://en.wikipedia.org/wiki/Even%E2%80%93odd_rule
[5] Computing area: http://geomalgorithms.com/a01-_area.html
[6] Line formula: http://geomalgorithms.com/a02-_lines.html